how to find a slant asymptote

Functions can 'get big' in different ways.

When they 'get big' by looking more and more like a 'slanted' line (i.e., not horizontal and not vertical),
then the function is said to have a slant asymptote.

Slant asymptotes are also called oblique asymptotes.

As discussed in Introduction to Asymptotes, an asymptote is a curve (usually a line)
that another curve gets arbitrarily close to as $\,x\,$ approaches $\,+\infty\,$, $\,-\infty\,$, or a finite number.

Here's how this general definition is 'specialized' to get a slant asymptote:

A 'slant asymptote' is a non-vertical, non-horizontal line
that another curve gets arbitrarily close to
as $\,x\,$ approaches $\,+\infty\,$ or $\,-\infty\,$.

What's the key to a slant asymptote situation?

The outputs are behaving more and more like $\,y = mx + b\,$ for $\,m\ne 0\,$
as inputs get arbitrarily large (big and positive, or big and negative).

This section gives a precise discussion of slant asymptotes,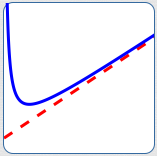
as well as conditions under which a rational function has a slant asymptote.

The red line is a slant asymptote
for the blue curve.

As $\,x\rightarrow\infty\,$,
the blue curve approaches the red line.

Conditions under which $\,y = mx + b\,$ ($\,m\ne 0\,$)

is a Slant Asymptote for a Function $\,f\,$

Let $\,f\,$ be a nonlinear function.
That is, $\,f(x)\,$ is not of the form $\,f(x) = cx + d\,$ for any real numbers $\,c\,$ and $\,d\,$.

Let $\,m \ne 0\,$.
The line $\,y = mx + b\,$ is a slant asymptote for $\,f\,$
if and only if at least one of the following conditions holds:

as $\,x\rightarrow\infty\,$, $\,f(x) - (mx + b) \rightarrow 0\,$
as $\,x\rightarrow -\infty\,$, $\,f(x) - (mx + b) \rightarrow 0\,$

That is, the vertical distance between the line $\,y = mx + b\,$ and the graph of $\,f\,$ approaches zero as $\,x\rightarrow\infty\,$ or $\,x\rightarrow -\infty\,$ (or both).

A function can have at most two slant asymptotes.
It can approach one line as $\,x\rightarrow\infty\,$, and a different line as $\,x\rightarrow -\infty\,$.
A function can have a slant asymptote and a horizontal asymptote.
For example, it might approach a horizontal line as $\,x\rightarrow\infty\,$, and a slanted line as $\,x\rightarrow -\infty\,$.

Example:
A Non-Rational Function with a Slant Asymptote

Let $\,f(x) = 3x + \text{e}^{-x}\,$ (the blue curve at right).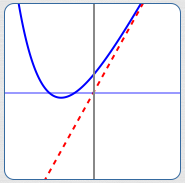
As $\,x\rightarrow \infty\,$, we have $\,\text{e}^{-x}\rightarrow 0\,$, so the outputs from $\,f\,$ are looking more and more like $\,3x\,$.
More precisely, as $\,x\rightarrow \infty\,$, we have: $$ \begin{gather} \cssId{s41}{f(x) - 3x \ = \ (3x + \text{e}^{-x}) - 3x \ = \ \text{e}^{-x}}\cr \cssId{s42}{\text{and}}\cr \cssId{s43}{\text{e}^{-x}\rightarrow 0} \end{gather} $$ Thus, $\,y = 3x\,$ (the red line at right) is a slant asymptote for $\,f\,$.

Example:
A Rational Function with a Slant Asymptote;
degree of numerator is exactly one greater than degree of denominator

Let $\displaystyle\,R(x) = \frac{x^2 - 4x - 5}{x - 3}\,$.

When $\,x\,$ is big, the outputs from $\,R(x)\,$ looks like $\,\frac{\text{big}}{\text{big}}\,$, which is not very useful.
As usual, we will rename the function to better understand what happens when $\,x\,$ is big:

The key is to do a long division:

	$x$	$-$	$1$
$x-3$	$x^2$	$-$	$4x$	$-$	$5$
	$-(x^2$	$-$	$3x$	$)$

			$-x$	$-$	$5$
		$-($	$-x$	$+$	$3)$

					$-8$

Thus, $$ \cssId{s54}{R(x)} \cssId{s55}{= \frac{x^2 - 4x - 5}{x - 3}} \ \ \cssId{s56}{=\ \ x - 1 \ \ \ + \overbrace{\left(\frac{-8}{x-3}\right)}^{\text{this part tends to zero}}} $$

Note that as $\,x\rightarrow\pm\infty\,$, $\displaystyle\,\frac{-8}{x-3}\rightarrow 0\,$.

Therefore, as inputs get big, the function is looking more and more like the line $\,y = x - 1\,$.
Thus, $\,y = x - 1\,$ is a slant asymptote for the function $\,R\,$.

The graph of the function $\,\color{blue}{R}\,$ (in blue), together with its slant asymptote $\,\color{red}{y = x - 1}\,$ (in red), is shown at right.

When we were doing the long division of $\,x^2 - 4x - 5\,$ by $\,x - 3\,$ up above,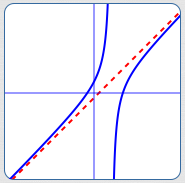
what caused the $\,x = x^1\,$ to appear in the quotient $\,x - 1\,$?
It was the fact that the degree of the numerator is one more than the degree of the denominator!
This is the key ingredient for determining if a rational function has a slant asymptote.
(There are a couple other technical requirements, which are stated below.)

In summary, we have:

Conditions under which
a Rational Function has a Slant Asymptote

Let $\,N(x)\,$ and $\,D(x)\,$ be polynomials, so that $\displaystyle\,R(x) = \frac{N(x)}{D(x)}\,$ is a rational function.

The function $\,R\,$ has a slant asymptote when the following conditions are met:

$\deg{N(x)} = \deg{D(x)} + 1$
(the degree of the numerator is exactly one more than the degree of the denominator)
$\deg{N(x)} \ge 2$
(the numerator is at least quadratic)
when dividing $\,D(x)\,$ into $\,N(x)\,$, the remainder is not zero

Why do we require that $\deg{N(x)}\ge 2\,$?
Notice that $\displaystyle \,y = \frac{x-1}{3}\,$ is a rational function, since both numerator and denominator are polynomials.
The degree of the numerator is $\,1\,$.
The degree of the denominator is $\,0\,$.
Thus, the degree of the numerator is exactly one more than the degree of the denominator.
However, this is just the linear function $\,y = \frac 13x - \frac 13\,$, which does not have a slant asymptote.
Why do we require the remainder to be nonzero?
Notice that $\displaystyle \,y = \frac{x^2-1}{x-1}\,$ is a rational function, and the degree of the numerator is exactly one more than the degree of the denominator.
However, in this case $\,x - 1\,$ goes into $\,x^2 - 1\,$ evenly (the remainder is zero): $$ \cssId{s87}{y = \frac{x^2-1}{x-1}} \cssId{s88}{= \frac{(x-1)(x+1)}{x-1}} \cssId{s89}{= x + 1\,,} \ \ \cssId{s90}{\text{for $\,x\ne 1\,$}} $$ This function graphs as a line that is punctured at $\,x = 1\,$. It does not have a slant asymptote.